Dijkstra-Algorithmus: Unterschied zwischen den Versionen

Aus SibiWiki
Zur Navigation springen Zur Suche springen
K (Akaibel verschob die Seite Dijkstra-Algorithmus ab Abi 2017 nach Dijkstra-Algorithmus)
Zeile 11: Zeile 11:


Der Dijkstra-Algorithmus bezieht sich auf die Datenstruktur [[Graph]].
Der Dijkstra-Algorithmus bezieht sich auf die Datenstruktur [[Graph]].
=Fachbegriffe=
Dijkstra-Algorithmus, rote Liste, gelbe Liste


= Idee des Dijkstra-Algorithmus=
= Idee des Dijkstra-Algorithmus=

Version vom 23. Juni 2019, 13:27 Uhr


Originalgraph
Ergebnis des Dijkstra-Algorithmus für Kassel

Mit Hilfe des Dijkstra-Algorithmus kann man für einen Startknoten die kürzesten Wege zu allen anderen Knoten des Graphen bestimmen.

Der Dijkstra-Algorithmus ist wesentlich effizienter als die Suche nach einem kürzesten Weg mithilfe von Backtracking

Der Dijkstra-Algorithmus bezieht sich auf die Datenstruktur Graph.

Fachbegriffe

Dijkstra-Algorithmus, rote Liste, gelbe Liste

Idee des Dijkstra-Algorithmus

Notwendige Datenstrukturen

  • Für jeden Knoten wird der Vorgänger und ein Wert distanz gespeichert; distanz gibt die bisher beste gefundene Distanz zum Startknoten an.
  • gelbe Liste: In dieser Liste werden Knoten gespeichert, für die schon ein Distanzwert vorliegt, deren Distanz zum Startknoten aber noch nicht abschließend festgelegt werden konnte. Die Knoten erscheinen in der gelben Liste gemäß ihrem Distanzwert, und zwar in aufsteigender Reihenfolge.
  • rote Liste: Man braucht eine Liste, in der alle Knoten gespeichert werden, deren Distanz zum Startknoten abschließend festgestellt wurde.


Algorithmus

  1. Die Distanz des Startknoten wird auf 0 gesetzt; der von allen anderen Knoten auf unendlich.
  2. Der Startknoten wird in die rote Liste eingefügt.
  3. Alle Nachbarknoten des Startknotens werden in die gelbe Liste eingefügt, und zwar gemäß ihrer Distanz zum Startknoten.
  4. Die folgenden Schritte laufen jetzt so lange, bis die gelbe Liste leer ist:
    1. den ersten Knoten aus der gelben Liste (im folgenden ersterGelber) entnehmen und in die rote Liste einfügen. Denn die Distanz dieses Knotens ist endgültig geklärt.
    2. für alle Nachbarknoten von ersterGelber überprüft man:
      1. wenn sie noch nicht in der gelben Liste sind: Distanz berechnen (=Distanz von ersterGelber plus Kantenlänge von ersterGelber) und dann in die gelbe Liste hinzufügen (=gemäß der Distanz einfügen)
      2. wenn sie schon in der gelben Liste sind: Überprüfen, ob die Distanz von ersterGelber plus Kantenlänge kleiner ist als die bisher gespeicherte Distanz: Dann hat man eine bessere Route gefunden! Die Distanz des Nachbarknoten wird dann entsprechend verbessert, wodurch sich seine Position in der gelben Liste verbessert.


Kürzester Weg für einen beliebigen Knoten

Die Distanz kann man direkt aus dem Knoten auslesen.

Den kürzesten Weg von einem beliebigen Knoten zum Startknoten kann man jetzt angeben, indem man sich von dem Knoten aus immer zum nächsten Vorgänger hangelt, bis mn schließlich beim Startknoten angekommen ist.

Beispiel

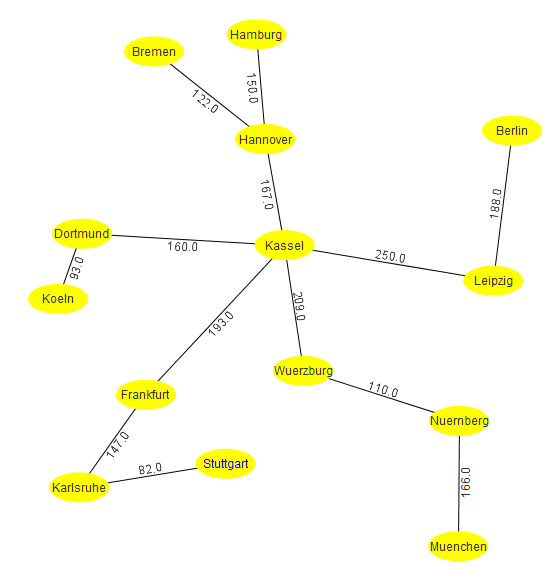
Für den Startknoten Kassel sind die ersten Schritte des Dijkstra-Algorithmus die folgenden.

  • Die rote Liste' ist fett geschrieben und ist von oben nach unten zu lesen.
  • Die gelbe Liste ist jeweils von links nach rechts zu lesen.
    • Veränderungen in der gelben Liste sind unterstrichen.

In der gelben Liste wird in Klammern die aktuelle Distanz zum Startknoten und der Vorgängerknoten (als Nummernschild) angegeben.

  • Kassel (0, --): Dortmund (160, KS), Hannover (167, KS), Frankfurt (193, KS), Wuerzburg (209, KS), Leipzig (250, KS)
  • Dortmund (160, KS): Hannover (167, KS), Frankfurt (193, KS), Wuerzburg (209, KS), Leipzig (250, KS), Koeln (253, DO), Bremen (394, DO)
  • Hannover (167, KS): Frankfurt (193, KS), Wuerzburg (209, KS), Leipzig (250, KS), Koeln (253, DO), Bremen (289, H), Hamburg (317, H), Berlin (457, H)
  • Frankfurt (193, KS): Wuerzburg (209, KS), Leipzig (250, KS), Koeln (253, DO), Bremen (289, H), Hamburg (317, H), Karlsruhe (340, F), Berlin (457, H)
  • Wuerzburg (209, KS): Leipzig (250, KS), Koeln (253, DO), Bremen (289, H), Hamburg (317, H), Nuernberg (319, WÜ), Karlsruhe (340, F), Berlin (457, H)
  • Leipzig (250, KS): Koeln (253, DO), Bremen (289, H), Hamburg (317, H), Nuernberg (319, WÜ), Berlin (438, L)
  • Koeln (253, DO): Bremen (289, H), Hamburg (317, H), Nuernberg (319, WÜ), Karlsruhe (340, F), Berlin (438, L)
  • Bremen (289, H): Hamburg (317, H), Nuernberg (319, WÜ), Karlsruhe (340, F), Berlin (438, L)
  • Hamburg (317, H): Nuernberg (319, WÜ), Karlsruhe (340, F), Berlin (438, L)
  • Nuernberg (319, WÜ): Karlsruhe (340, F), Berlin (438, L), Muenchen (485, N), Stuttgart (527, N)
  • Karlsruhe (340, F): Stuttgart (422, KA), Berlin (438, L), Muenchen (485, N)
  • Stuttgart (422, KA): Berlin (438, L), Muenchen (485, N)
  • Berlin (438, L): Muenchen (485, N)
  • Muenchen (485, N)


Den kürzesten Weg von Kassel nach Stuttgart findet man jetzt, indem man in der roten Liste Stuttgart sucht und dann in der roten Liste "rückwärts" geht:

Stuttgart (422, KA) -> Karlsruhe (340, F) -> Frankfurt (193, KS) -> Kassel (0, --)

Implementierung

Diese Implementierung umfasst zwei Klassen:

  • DijkstraAlgorithmus
  • DijkstraNode

Die Klasse DijkstraAlgorithmus enthält eine (lange...) Methode initGraph, damit man das Ganze auch testen kann.


Klasse DijkstraAlgorithmus: 

import graph.Graph;
import graph.GraphWithViewer;
import gui.GUI;
import linear.List;
import linear.ListWithViewer;

public class DijkstraAlgorithmus {
   public GraphWithViewer graph;
   List<DijkstraNode> gelbeListe;
   List<DijkstraNode> roteListe;

   public DijkstraAlgorithmus(){
       initGraph();
   }

   public void dijkstra(String pStadt) {
        gelbeListe = new ListWithViewer<>();
        roteListe = new ListWithViewer<>();
        DijkstraNode startNode = (DijkstraNode)graph.getNode(pStadt);
        startNode.setDistanz(0);
        gelbeListe.append(startNode);
        while(!gelbeListe.isEmpty()){
           gelbeListe.toFirst();
           DijkstraNode ersterGelber = gelbeListe.getContent();
           //System.out.println("ersterGelber: "+ersterGelber);
           gelbeListe.remove();
           ersterGelber.mark();
           roteListe.append(ersterGelber);
           List<GraphNode> nachbarn = graph.getNeighbours(ersterGelber);
           nachbarn.toFirst();
           while(nachbarn.hasAccess()){
              DijkstraNode derNachbar = (DijkstraNode) nachbarn.getContent();
              if (!derNachbar.isMarked()) {
               //System.out.println("currentNeighbour: "+currentNeighbour);
               double streckeErsterZumNachbar = graph.getEdgeWeight(ersterGelber, derNachbar);
               if (ersterGelber.getDistanz() + streckeErsterZumNachbar < derNachbar.getDistanz()) {
                   // ueber derNachbar fuehrt eine kuerzere Strecke zu currentNeighbour!
                   derNachbar.setVorgaenger(ersterGelber);
                   derNachbar.setDistanz(ersterGelber.getDistanz() + streckeErsterZumNachbar);
                   inGelbeListeUpdaten(derNachbar);
               }
           }
           nachbarn.next();
           }
        }
     }

   /**
    * sorgt dafuer, dass node gemaess seiner Distanz
    * die richtige Position in gelbeListe bekommt.
    * wenn pNode noch gar nicht in gelbeListe enthalten ist,
    * dann wird node an der richtigen Stelle eingefuegt.
    */
   private void inGelbeListeUpdaten(DijkstraNode pNode) {
       boolean inserted = false;
       gelbeListe.toFirst();
       while(gelbeListe.hasAccess()){
           DijkstraNode aktuell = gelbeListe.getContent();
           if(aktuell.getDistanz() >= pNode.getDistanz()){
               gelbeListe.insert(pNode);
               inserted = true;
               break;
           }
           gelbeListe.next();
       }
       if(inserted){
           // ggf. taucht pNode nochmal in der Liste auf!
           // dann muss er entfernt werden!
           while(gelbeListe.hasAccess()){
               DijkstraNode aktuell = gelbeListe.getContent();
               if(aktuell.getName().equals(pNode.getName())){
                   gelbeListe.remove();
                   break;
               }
               gelbeListe.next();
           }
       }
       else{
           // der Knoten wurde noch nicht eingefuegt!
           gelbeListe.append(pNode);
       }
   }     

   /**
    * erzeugt einen Graph, in dem nur die Dijkstra-Verbindungen eingetragen sind
    * @param pGraph
    * @param roteListe
    * @return
    */
   public GraphWithViewer zeigeDijkstraGraph(){
       Graph pGraph = graph;
       GraphWithViewer ergebnis = new GraphWithViewer();
       List<GraphNode> nodes = pGraph.getNodes();
       for(nodes.toFirst(); nodes.hasAccess(); nodes.next()){
           ergebnis.addNode((DijkstraNode) nodes.getContent());
       }
       for(roteListe.toFirst(); roteListe.hasAccess(); roteListe.next()){
           DijkstraNode aktuell = roteListe.getContent();
           DijkstraNode vorgaenger = aktuell.getVorgaenger();
           if(vorgaenger != null){
               double distanz = pGraph.getEdgeWeight(pGraph.getNode(aktuell.getName()), pGraph.getNode(vorgaenger.getName()));
               ergebnis.addEdge(ergebnis.getNode(aktuell.getName()),
                       ergebnis.getNode(vorgaenger.getName()),
                       distanz);
           }
       }
       ergebnis.switchToISOMLayout();
       return ergebnis;
   }

   private void initGraph(){
       graph = new GraphWithViewer();

       DijkstraNode dortmund = new DijkstraNode("Dortmund");
       graph.addNode(dortmund);
       DijkstraNode koeln = new DijkstraNode("Koeln");
       graph.addNode(koeln);
       DijkstraNode frankfurt = new DijkstraNode("Frankfurt");
       graph.addNode(frankfurt);
       DijkstraNode kassel = new DijkstraNode("Kassel");
       graph.addNode(kassel);
       DijkstraNode wuerzburg = new DijkstraNode("Wuerzburg");
       graph.addNode(wuerzburg);
       DijkstraNode bielefeld = new DijkstraNode("Bielefeld");
       DijkstraNode hamburg = new DijkstraNode("Hamburg");
       graph.addNode(hamburg);
       DijkstraNode berlin = new DijkstraNode("Berlin");
       graph.addNode(berlin);
       DijkstraNode bremen = new DijkstraNode("Bremen");
       graph.addNode(bremen);
       DijkstraNode hannover = new DijkstraNode("Hannover");
       graph.addNode(hannover);
       DijkstraNode leipzig = new DijkstraNode("Leipzig");
       graph.addNode(leipzig);
       DijkstraNode nuernberg = new DijkstraNode("Nuernberg");
       graph.addNode(nuernberg);
       DijkstraNode stuttgart = new DijkstraNode("Stuttgart");
       graph.addNode(stuttgart);
       DijkstraNode muenchen = new DijkstraNode("Muenchen");
       graph.addNode(muenchen);
       DijkstraNode karlsruhe = new DijkstraNode("Karlsruhe");
       graph.addNode(karlsruhe);

       graph.addEdge(kassel, dortmund, 160);
       graph.addEdge(dortmund, koeln, 93);
       graph.addEdge(frankfurt, kassel, 193);
       graph.addEdge(kassel, wuerzburg, 209);
       graph.addEdge(wuerzburg, frankfurt, 119);
       graph.addEdge(frankfurt, koeln, 189);
       graph.addEdge(berlin, hamburg, 289);
       graph.addEdge(hamburg, bremen, 119);
       graph.addEdge(bremen, hannover, 122);
       graph.addEdge(hannover, hamburg, 150);
       graph.addEdge(berlin, hannover, 290);
       graph.addEdge(berlin, leipzig, 188);
       graph.addEdge(hannover, kassel, 167);
       graph.addEdge(leipzig, kassel, 250);
       graph.addEdge(dortmund, bremen, 234);
       graph.addEdge(dortmund, hannover, 210);
       graph.addEdge(leipzig, nuernberg, 278);
       graph.addEdge(wuerzburg, nuernberg, 110);
       graph.addEdge(nuernberg, muenchen, 166);
       graph.addEdge(muenchen, stuttgart, 223);
       graph.addEdge(nuernberg, stuttgart, 208);
       graph.addEdge(stuttgart, karlsruhe, 82);
       graph.addEdge(karlsruhe, frankfurt, 147);
 
       // auf ein geeignetes Layout umstellen
       graph.switchToISOMLayout();
   }
 
   public static void main(String[] args) {
       DijkstraAlgorithmus da = new DijkstraAlgorithmus();
       new GUI(da);
   }
}


Klasse DijkstraNode: 

import graph.GraphNode;

public class DijkstraNode extends GraphNode{

 private DijkstraNode vorgaenger;
 private double distanz;
 
 public DijkstraNode(String pName) {
       super(pName);
       vorgaenger = null;
       distanz = 100000000;
   }

 public void setDistanz(double pDistanz){
    this.distanz = pDistanz;
 }

 public double getDistanz(){
    return distanz;
 }

 public void setVorgaenger(DijkstraNode pNode){
    this.vorgaenger = pNode;
 }

 public DijkstraNode getVorgaenger() {
    return vorgaenger;
 }

 public String toString(){
        String ergebnis = this.getName()+": "+this.distanz;
        if(this.vorgaenger != null){
            ergebnis += (" ("+vorgaenger.getName()+")");
        }
        return ergebnis;
     }     
 }

Abgerufen von „https://sibiwiki.de/wiki/index.php?title=Dijkstra-Algorithmus&oldid=2902“